
Point Cloud Downsampling Methods
Point Cloud Downsampling Methods for Structural Analysis: A Comprehensive Review
Preface
This article provides a comprehensive review of point cloud downsampling methods with a specific focus on structural analysis applications. We analyze both classical and state-of-the-art approaches, evaluating their advantages, limitations, computational efficiency, and suitability for preserving structural features. This review aims to guide researchers and practitioners in selecting appropriate downsampling techniques for structural engineering applications.
Point clouds obtained from LiDAR, photogrammetry, or other 3D scanning technologies often contain millions or billions of points, making them computationally expensive to process. Downsampling reduces data size while preserving essential geometric information, particularly critical for structural analysis where feature preservation directly impacts analytical accuracy.
1. Comparative Analysis for Structural Applications
| Method | Structural Feature Preservation | Computational Efficiency | Implementation Complexity | Noise Robustness |
|---|---|---|---|---|
| Voxel Grid | Medium | High | Low | Medium |
| Random | Low | Very High | Very Low | Low |
| FPS | Medium-High | Low | Medium | Medium |
| Normal-Based | High | Medium | Medium-High | Low-Medium |
| Curvature-Based | Very High | Low | High | Low |
| Octree | Medium-High | Medium-High | Medium | Medium-High |
| Semantic-Guided | Very High | Low | Very High | Medium-High |
Visualization
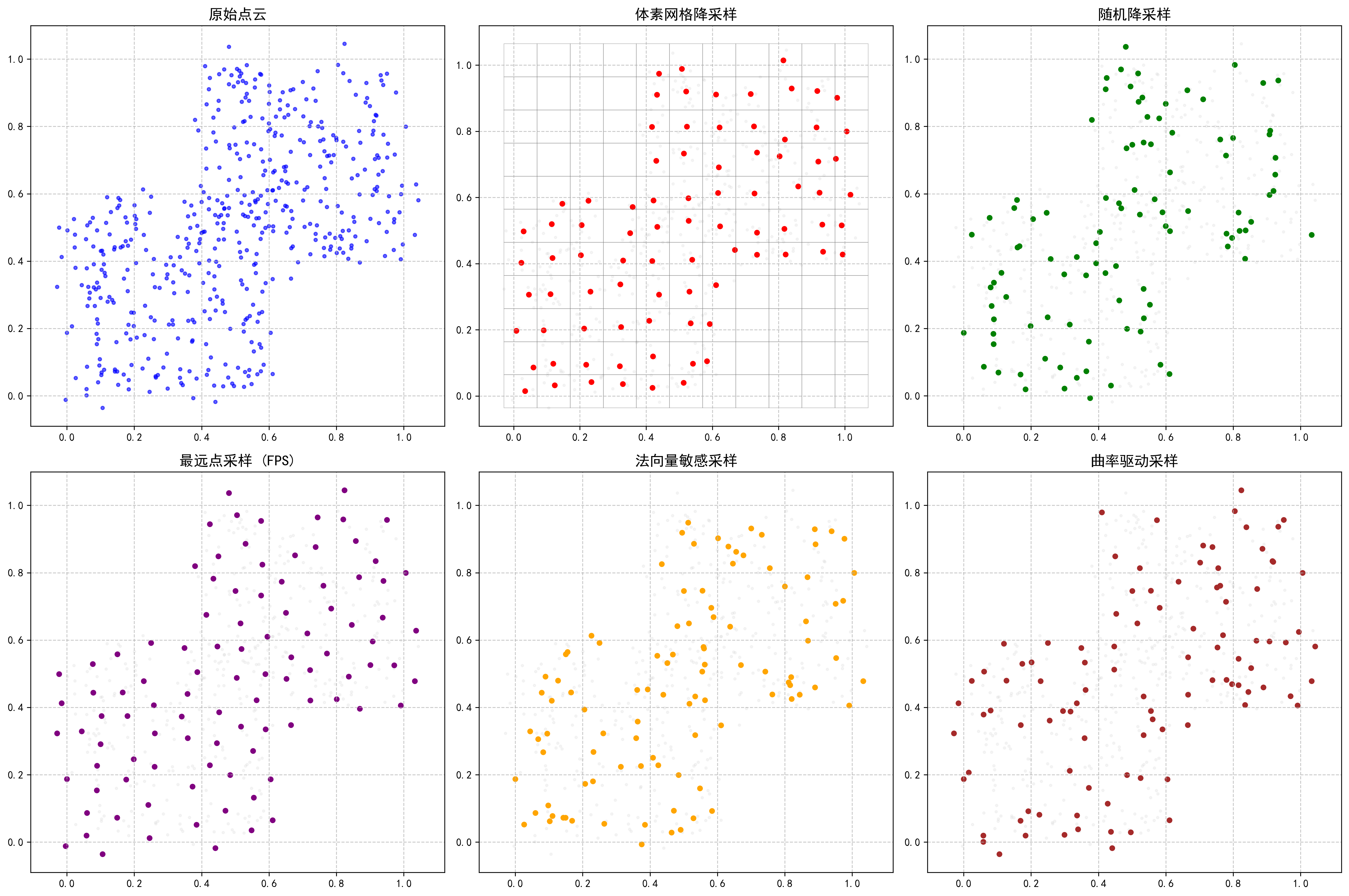
2. Classical Downsampling Methods
2.1 Voxel Grid Downsampling
Principle: Divides the point cloud into equally sized 3D voxels and replaces all points within each voxel with their centroid.
Advantages:
- Uniform spatial distribution of points
- Preserves overall geometry
- Computationally efficient (O(n))
- Simple implementation
Limitations:
- May lose fine details at structural connections
- Fixed voxel size can be problematic for varying density regions
- Sharp edges may be smoothed
Parameter Sensitivity: Voxel size (typically in meters) directly controls the downsampling ratio and detail preservation.
2.2 Random Downsampling
Principle: Randomly selects a subset of points from the original cloud.
Advantages:
- Extremely fast computation
- Simple implementation
Limitations:
- No spatial distribution guarantee
- May create uneven representation of structural elements
- Critical structural features may be lost randomly
2.3 Uniform Sampling
Principle: Ensures points are distributed with approximately equal spacing.
Advantages:
- Maintains consistent point density
- Better than random sampling for structural analysis
Limitations:
- May still miss important structural features
- Less adaptive to varying complexity regions
2.4 Farthest Point Sampling (FPS)
Principle: Iteratively selects points that are farthest from the already selected point set.
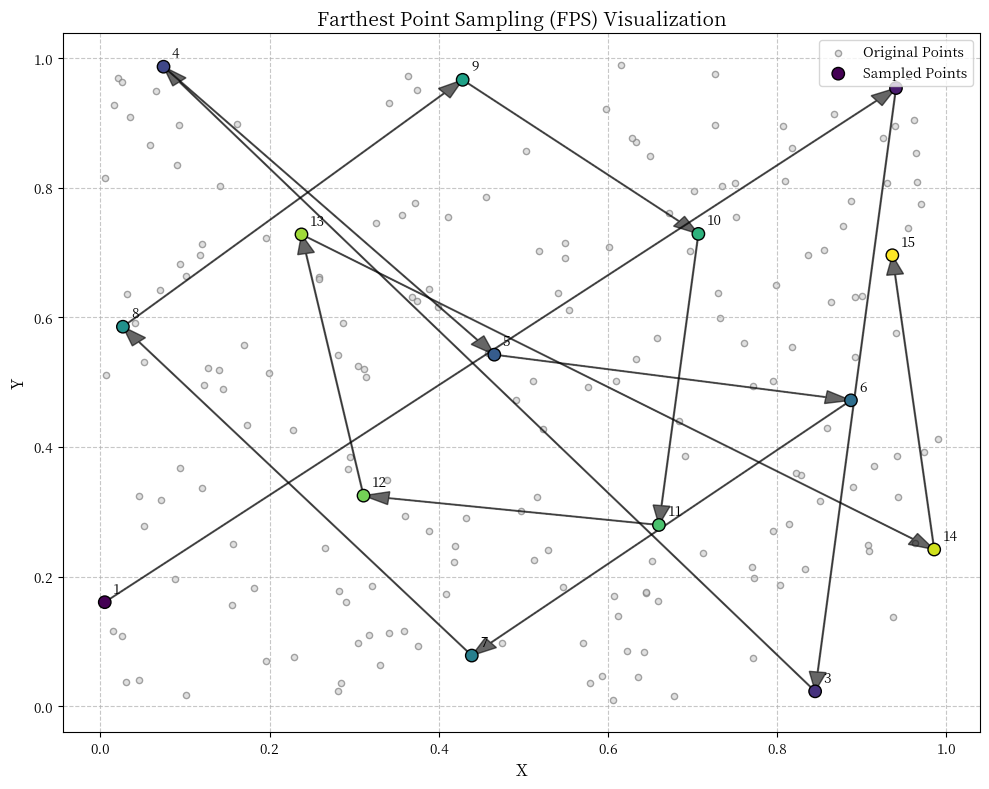
Advantages:
- Preserves overall shape effectively
- Better coverage of the entire structure
- Maintains structural extremities
Limitations:
- Computationally expensive (O(n²) naive implementation)
- May undersample dense regions with important structural details
3. Advanced Downsampling Methods
3.1 Normal-Based Sampling
Principle: Preserves points based on surface normal variations, retaining more points in high-curvature regions.
Advantages:
- Preserves structural edges and corners
- Adaptive to geometric complexity
- Maintains critical structural features
Limitations:
- Requires accurate normal estimation
- More computationally intensive
- Parameter tuning can be challenging
3.2 Curvature-Based Sampling
Principle: Retains more points in regions with high curvature.
Advantages:
- Excellent preservation of structural details
- Adaptive to local geometry
- Ideal for structures with varying complexity
Limitations:
- Computationally expensive
- Sensitive to noise
- Requires curvature estimation preprocessing
3.3 Feature-Preserving Sampling
Principle: Identifies and preserves key structural features (edges, corners, joints) during downsampling.
Advantages:
- Maintains critical structural elements
- Optimized for structural analysis applications
- Better preservation of connectivity information
Limitations:
- Complex implementation
- Feature detection may be error-prone
- Higher computational cost
3.4 Deep Learning-Based Methods
Principle: Uses neural networks to learn optimal sampling strategies from training data.
Advantages:
- Can learn domain-specific features
- Potentially superior feature preservation
- Adaptable to specific structural types
Limitations:
- Requires training data
- Black-box nature
- Computational overhead for inference
- May not generalize well to unseen structures
4. Hierarchical and Multi-Resolution Methods
4.1 Octree-Based Sampling
Principle: Recursively subdivides space into octants, with subdivision depth based on point density.
Advantages:
- Multi-resolution representation
- Adaptive to local density
- Efficient spatial queries
- Memory efficient
Limitations:
- May create artifacts at octree boundaries
- Implementation complexity
- Parameter tuning required
4.2 Progressive Sampling
Principle: Creates multiple resolution levels that can be used progressively.
Advantages:
- Allows multi-resolution analysis
- Enables progressive loading for visualization
- Adaptable detail level based on computational resources
Limitations:
- Storage overhead for multiple resolutions
- Complexity in implementation
5. Structural-Specific Downsampling Methods
5.1 Skeleton-Aware Downsampling
Principle: Preserves the skeletal structure of the building or infrastructure.
Advantages:
- Maintains structural load paths
- Preserves topological connections
- Optimized for structural analysis
Limitations:
- Requires skeleton extraction preprocessing
- Domain-specific implementation
5.2 Semantic-Guided Downsampling
Principle: Uses semantic segmentation to guide the sampling process, preserving different structural elements differently.
Advantages:
- Context-aware downsampling
- Can preserve critical structural components
- Adaptable to different structural element types
Limitations:
- Requires semantic segmentation
- More complex pipeline
- Potential segmentation errors propagate to sampling
6. Visualization Examples
The following diagrams illustrate the effects of different downsampling methods on a structural element:
Original Point Cloud (10,000 points)
↙️ ↘️ ↘️
Voxel Grid Random Normal-Based
(2,000 points) (2,000 points) (2,000 points)
8. Practical Recommendations
For structural analysis applications, we recommend:
- General purpose: Voxel grid downsampling with carefully selected voxel size
- Detail-critical applications: Normal or curvature-based methods
- Large-scale structures: Octree-based or hierarchical methods
- Structural health monitoring: Feature-preserving or semantic-guided methods
- Real-time applications: Optimized FPS or voxel grid implementations
9. Conclusion
Point cloud downsampling for structural analysis requires balancing computational efficiency with the preservation of structurally significant features. While voxel grid downsampling remains the most widely used method due to its simplicity and efficiency, advanced methods like feature-preserving and semantic-guided approaches offer superior results for critical structural applications. The selection of an appropriate method should consider the specific requirements of the structural analysis task, computational constraints, and the characteristics of the structure being analyzed.

